前言
最近发现 HRL (Hierarchical Reinforcement Learning) 似乎是一个非常有趣的研究方法,这里汇总了自己调研的几篇经典文章与心得体会
真是越看越心酸,前一阵子洗澡时想到可以在学习出的 RL agent 上再套一个 RL算法来学习,结果发现这正是 HRL 的思路😂
目录
- Learning Representations in Model-Free Hierarchical Reinforcement Learning
- Hierarchical Deep Reinforcement Learning Integrating Temporal Abstraction and Intrinsic Motivation
Learning Representations in Model-Free Hierarchical Reinforcement Learning
论文的研究动机是通过引入 HRL 来解决 RL 面对具有 Sparse Reward 的问题表现不佳的问题(个人感觉这是在使用另一种方式去解决 NeSy 方法在做的事情,都是引入抽象的特征表示)
Method
论文采用的方法框架由一个生产 sub goal 的 Meta-Controller 和一个解决 sub goal 的 Controller 组成
在时间 t 时,Meta-Controller 接收环境状态 $s_t$ 并选择一个 sub goal $g_t \in \mathcal{G}$ ,Controller 接收环境状态 $s_t$ 和 sub goal $g_t$ 并选择一个动作 $a_t$
对于 controller,它的奖励函数可以表示为
$$ G_t = \sum_{k=t}^{t + T} \gamma^{k-t} r'_{t}(g) $$其中 $r'_t(g)$ 是一个内部奖励函数,文章中似乎用来衡量 sub goal 是否达成
同样,对于 meta-controller,它的奖励函数可以表示为
$$ G_t = \sum_{k=t}^{t + N} \gamma^{k-t} r_k $$从定义中也可以推断出,当我们设计 Q 函数时,Controller 的 Q 函数需要考虑 sub goal 的影响,可以表示为 $Q_1(s, a, g)$;而 Meta-Controller 的 Q 函数则可以简单的表示为 $Q_2(s, g)$ (将 g 看作 Meta 层面的动作)
如果我们将神经网络的参数用 $\mathcal{W}$ 来表示的话,两种 Controller 的 loss function 可以表示为
$$\mathcal{L}_{meta}(\mathcal{W}_1) = \mathbb{E}_{s, g, G, s'} \left[ \left( G + \gamma \max_{g'} Q_1(s', g'; \mathcal{W}_1) - Q_1(s, g; \mathcal{W}_1) \right)^2 \right]$$$$\mathcal{L}_{controller}(\mathcal{W}_2) = \mathbb{E}_{s, g, a, r', s'} \left[ \left( r' + \gamma \max_{a'} Q_2(s', g, a'; \mathcal{W}_2) - Q_2(s, g, a; \mathcal{W}_2) \right)^2 \right]$$其中 $G$ 是 Meta-Controller 的回报
整个算法的流程图如下:

补充:作者在后面提到的 Intrinsic Motivation Learning 感觉是一个 reward hacking 的方法,并不具有普适性和特别的创新点
再补充:纯诈骗犯啊我服了,轻轻的一句 “For now, we assume that the subgoal, g ∈ G, is provided by an oracle (standing in for the meta-controller), and we focus only on learning to achieve this subgoal.” 就把如何设计 sub goal 的问题给带过了 😂 (不是,标题中写的清清楚楚的 Learning representations 跑哪去了)
Hierarchical Deep Reinforcement Learning Integrating Temporal Abstraction and Intrinsic Motivation
文章提出 h-DQN (Hierarchical Deep Q-Network) 来解决 RL 中的 Sparse Reward 问题
Method
h-DQN 由两个层次的 RL 组成,Meta-Controller 和 Controller,Meta-Controller 负责选择 sub goal,Controller 负责执行 sub goal
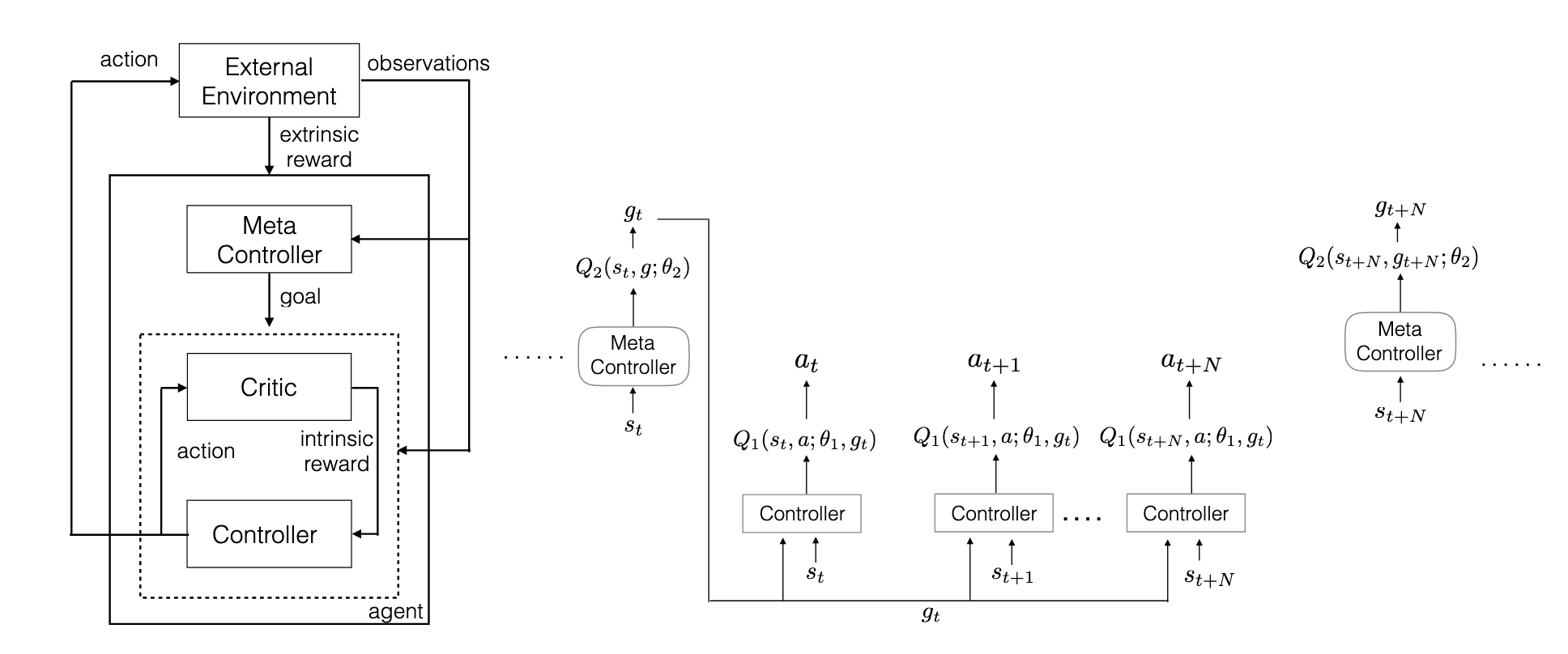
论文核心方法上面的图片就展现了出来,Meta-Controller 和 Contorller 更新的时间尺度是不一样的
Loss Function Meta-Controller 的 loss function 为
$$\mathcal{L}(\theta) = \mathbb{E}_{(s, g, G, s')} \left[ \left( G + \gamma \max_{g'} Q_1(s', g'; \theta) - Q_1(s, g; \theta) \right)^2 \right]$$Controller 的 loss function 为
$$\mathcal{L}(\theta) = \mathbb{E}_{(s, g, a, r, s')} \left[ \left( r + \gamma \max_{a'} Q_2(s', g, a'; \theta) - Q_2(s, g, a; \theta) \right)^2 \right]$$